SVGnest Save
An open source vector nesting tool
SVGNest: A browser-based vector nesting tool.
Demo: http://svgnest.com
(requires SVG and webworker support). Mobile warning: running the demo is CPU intensive.
references (PDF):
What is "nesting"?
Given a square piece of material and some letters to be laser-cut:

We want to pack all the letters into the square, using as little material as possible. If a single square is not enough, we also want to minimize the number of squares used.
In the CNC world this is called "nesting", and software that does this is typically targeted at industrial customers and very expensive.
SVGnest is a free and open-source alternative that solves this problem with the orbital approach outlined in [E.K. Burke et al. 2006], using a genetic algorithm for global optimization. It works for arbitrary containers and concave edge cases, and performs on-par with existing commercial software.
It also features part-in-part support, for placing parts in the holes of other parts.
Usage
Make sure all parts have been converted to outlines, and that no outlines overlap. Upload the SVG file and select one of the outlines to be used as the bin.
All other outlines are automatically processed as parts for nesting.
Outline of algorithm
While good heuristics exist for the rectangular bin packing problem, in the real world we are concerned with irregular shapes.
The strategy is made of two parts:
- the placement strategy (ie. how do I insert each part into a bin?)
- and the optimization strategy (ie. what's the best order of insertions?)
Placing the part
The key concept here is the "No Fit Polygon".
Given polygons A and B, we want to "orbit" B around A such that they always touch but do not intersect.
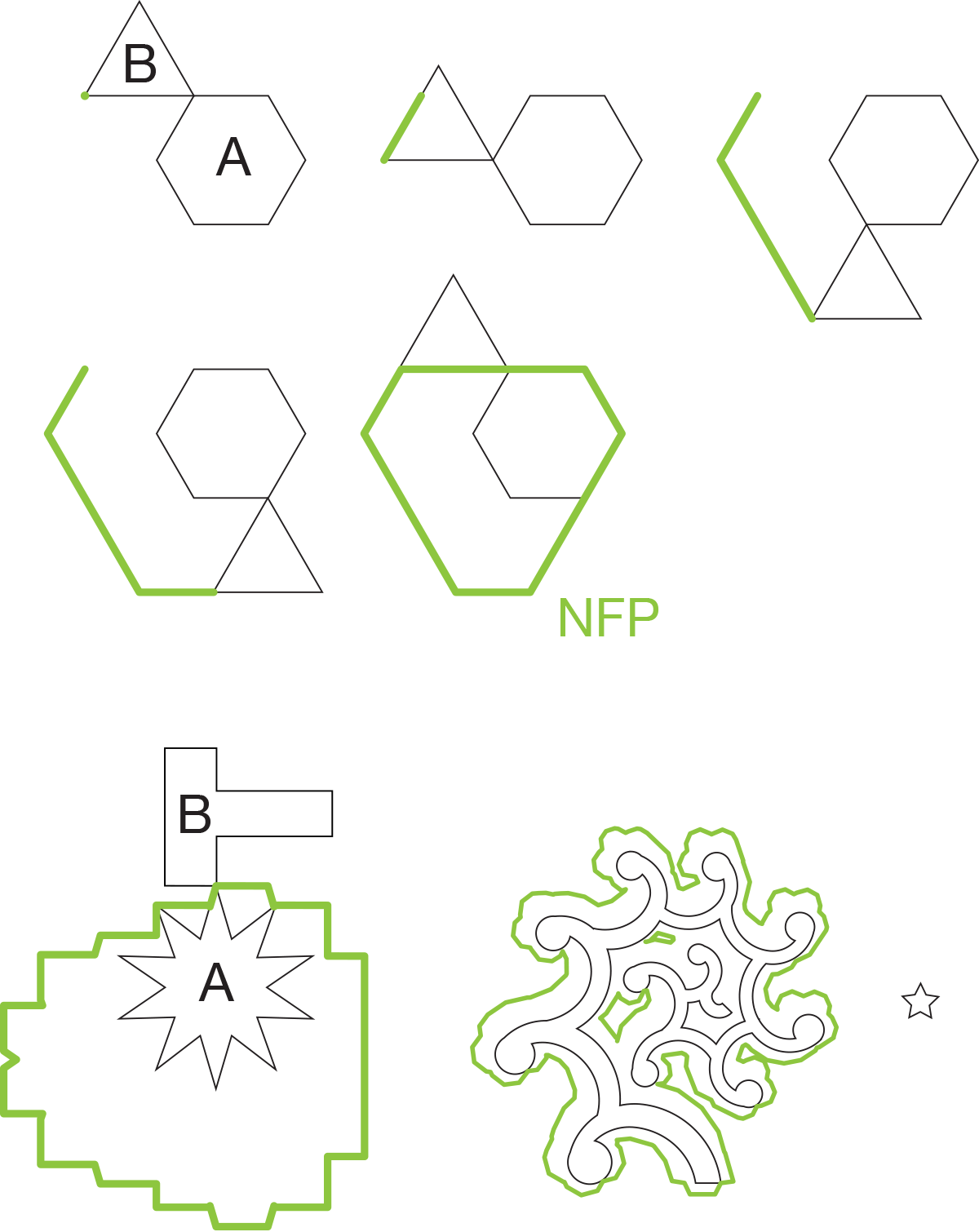
The resulting orbit is the NFP. The NFP contains all possible placements of B that touches the previously placed parts. We can then choose a point on the NFP as the placement position using some heuristics.
Similarly we can construct an "Inner Fit Polygon" for the part and the bin. This is the same as the NFP, except the orbiting polygon is inside the stationary one.
When two or more parts have already been placed, we can take the union of the NFPs of the previously placed parts.
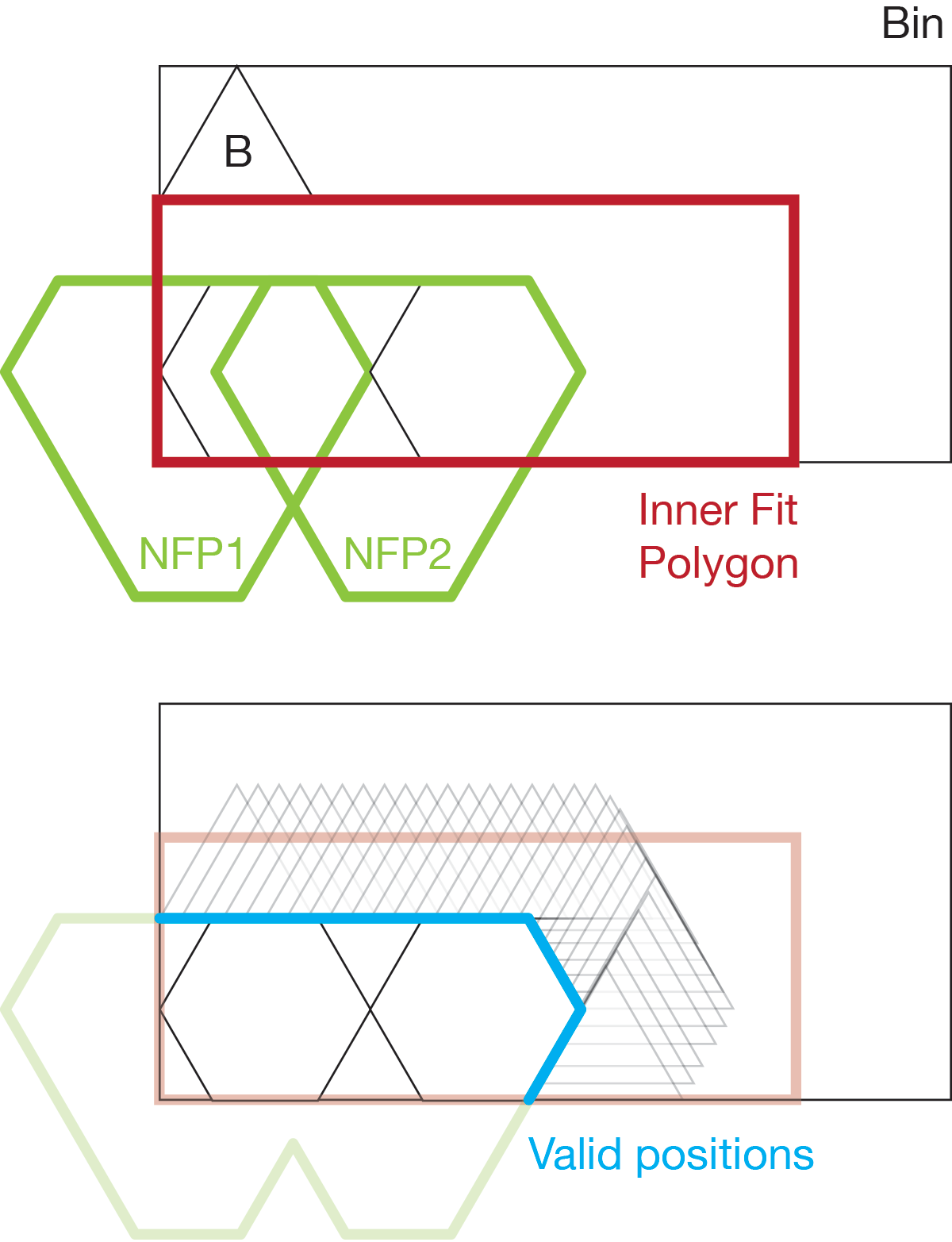
This means that we need to compute O(nlogn) NFPs to complete the first packing. While there are ways to mitigate this, we take the brute-force approach which has good properties for the optimization algo.
Optimization
Now that we can place the parts, we need to optimize the insertion order. Here's an example of a bad insertion order:
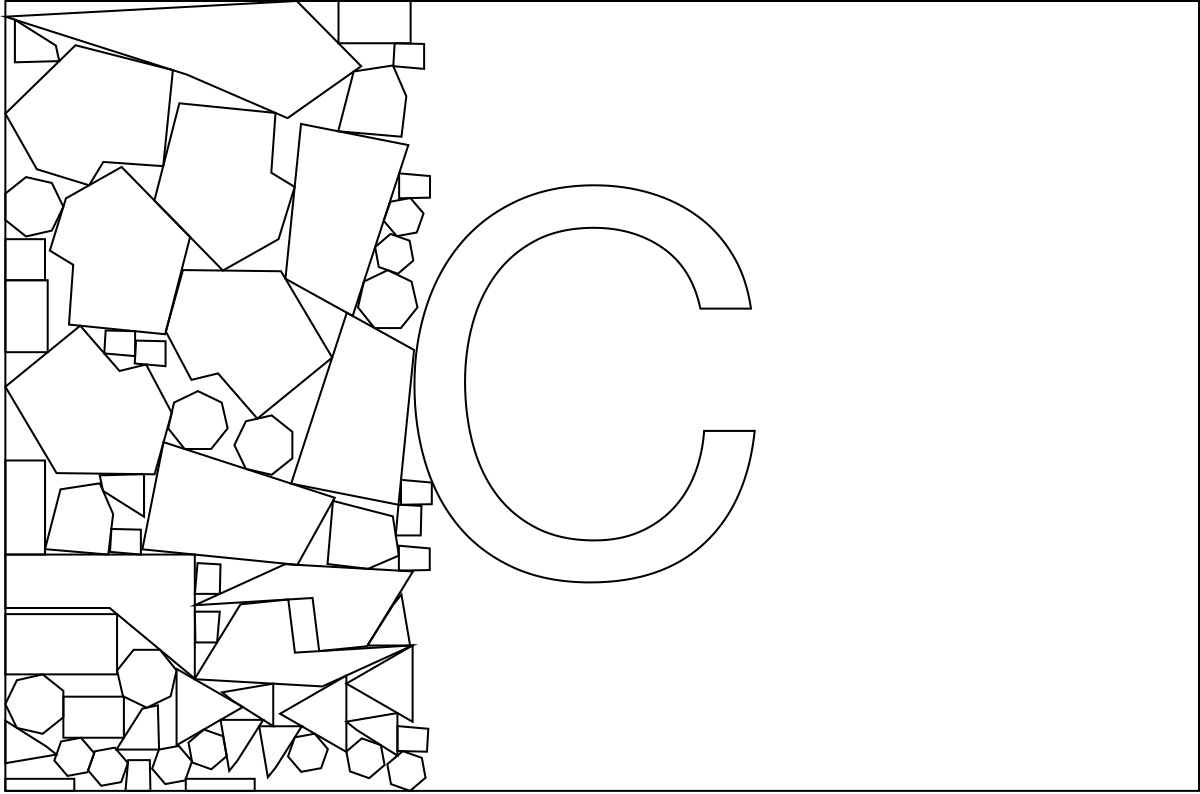
If the large "C" is placed last, the concave space inside it won't be utilized because all the parts that could have filled it have already been placed.
To solve this, we use the "first-fit-decreasing" heuristic. Larger parts are placed first, and smaller parts last. This is quite intuitive, as the smaller parts tend to act as "sand" to fill the gaps left by the larger parts.
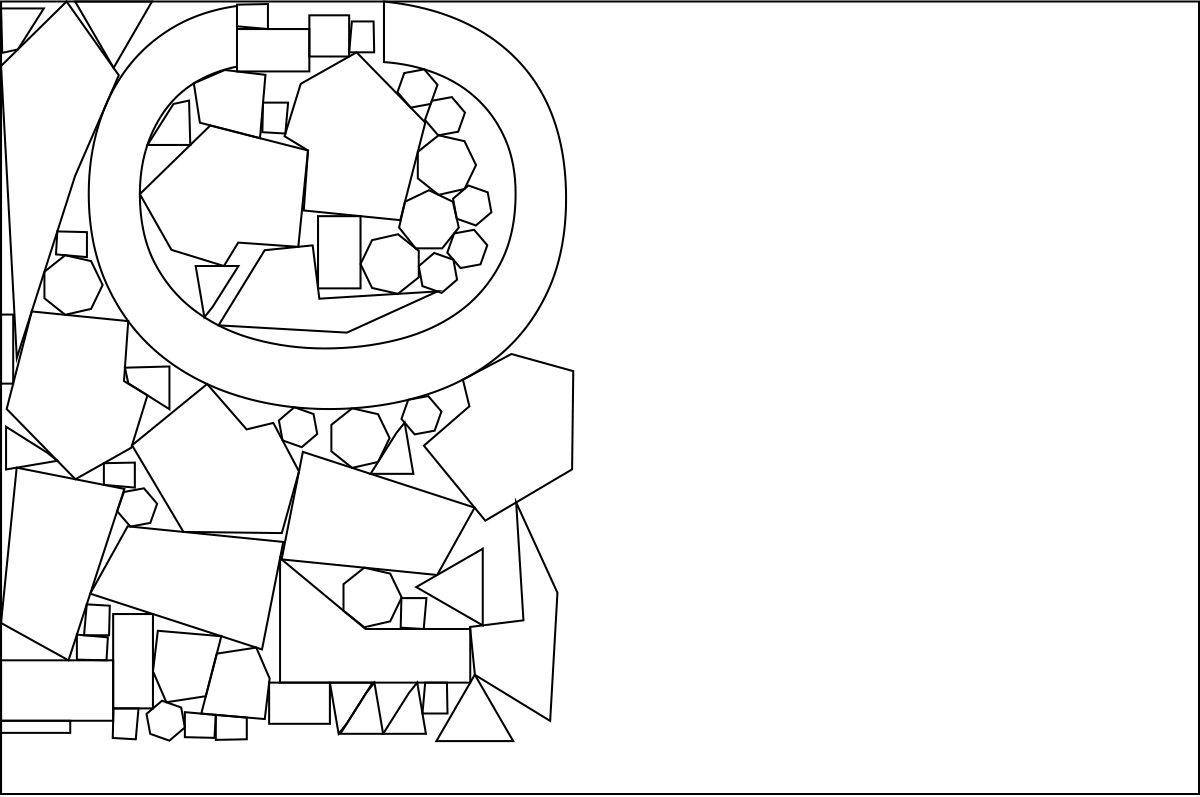
While this strategy gives us a good start, we want to explore more of the solution space. We could simply randomize the insertion order, but we can probably do better with a genetic algorithm. (If you don't know what a GA is, this article is a very approachable read)
Evaluating fitness
In our GA the insertion order and the rotation of the parts form the gene. The fitness function follows these rules:
- Minimize the number of unplaceable parts (parts that cannot fit any bin due to its rotation)
- Minimize the number of bins used
- Minimize the width of all placed parts
The third one is rather arbitrary, as we can also optimize for rectangular bounds or a minimal concave hull. In real-world use the material to be cut tends to be rectangular, and those options tend to result in long slivers of un-used material.
Because small mutations in the gene cause potentially large changes in overall fitness, the individuals of the population can be very similar. By caching NFPs new individuals can be evaluated very quickly.
Performance
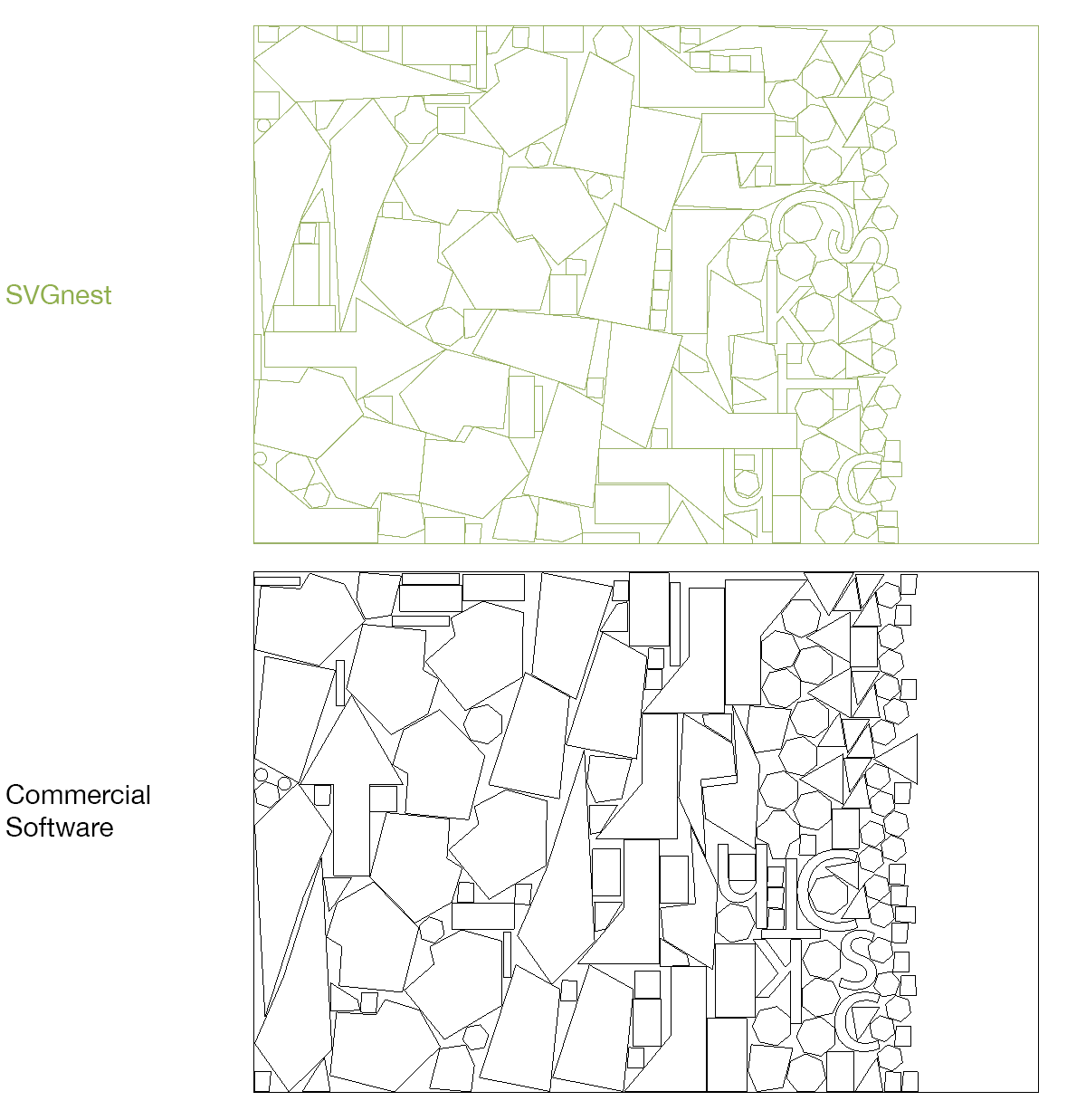
Performs similarly to commercial software, after both have run for about 5 minutes.
Configuration parameters
- Space between parts: Minimum space between parts (eg. for laser kerf, CNC offset etc.)
- Curve tolerance: The maximum error allowed for linear approximations of Bezier paths and arcs, in SVG units or "pixels". Decrease this value if curved parts appear to slightly overlap.
- Part rotations: The possible number of rotations to evaluate for each part. eg. 4 for only the cardinal directions. Larger values may improve results, but will be slower to converge.
- GA population: The population size for the Genetic Algorithm
- GA mutation rate: The probability of mutation for each gene or part placement. Values from 1-50
- Part in part: When enabled, places parts in the holes of other parts. This is off by default as it can be resource intensive
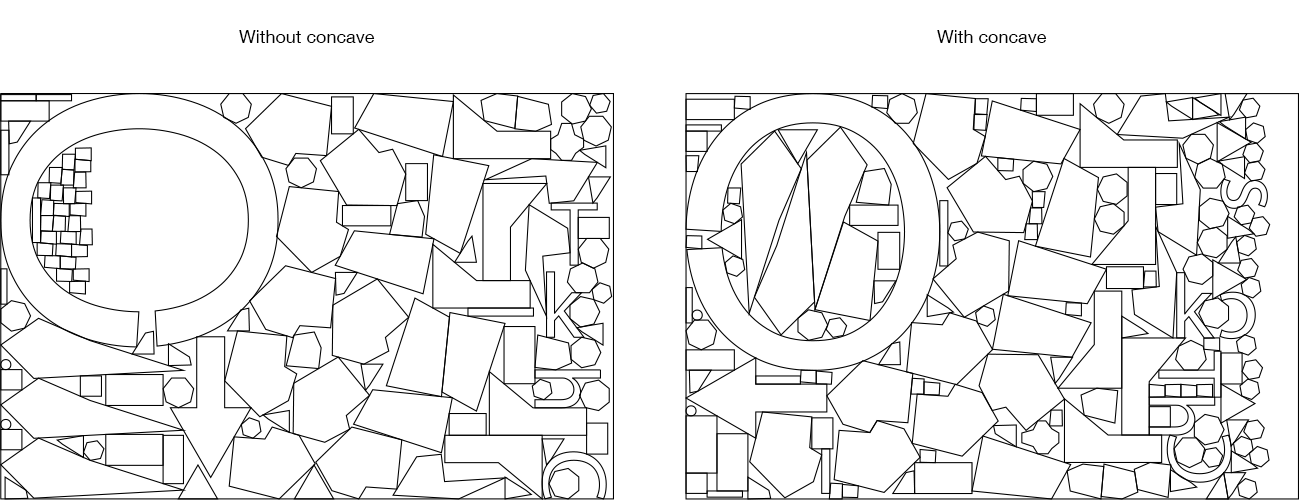
- Explore concave areas: When enabled, solves the concave edge case at a cost of some performance and placement robustness:
To-do
-
Recursive placement (putting parts in holes of other parts) - Customize fitness function (gravity direction, etc)
- kill worker threads when stop button is clicked
- fix certain edge cases in NFP generation

